Capitulo
4.3
![]()
Contenido página
Introducción
Esfuerzo elástico (stress)
deformación (strain)
constantes elásticas
Ondas sísmicas Comportamiento
Métodos sísmicos: Introducción
Métodos sísmicos: Introducción
Los métodos de exploración sísmicos se basan en la generación de ondas sísmicas
por ejemplo por medio de una explosión o por medio de un rompedor de caída.
Las ondas sísmicas son ondas mecánicas y elásticas, pues que las ondas sísmicas
causan deformaciones no permanentes en el medio, en que se propagan. La
deformación se constituye de una alternancia de compresión y de dilatación
de tal manera que las partículas del medio se acercan y se alejan respondiendo
a las fuerzas asociadas con las ondas, como por ejemplo en un elástico extendido.
Su propagación se describe por la ecuación de ondas. La velocidad de la
onda sísmica depende de los parámetros elásticos del medio, en que se propaga
la onda.
Esfuerzo elástico o tensión (stress),
deformación (strain) y las constantes elásticas
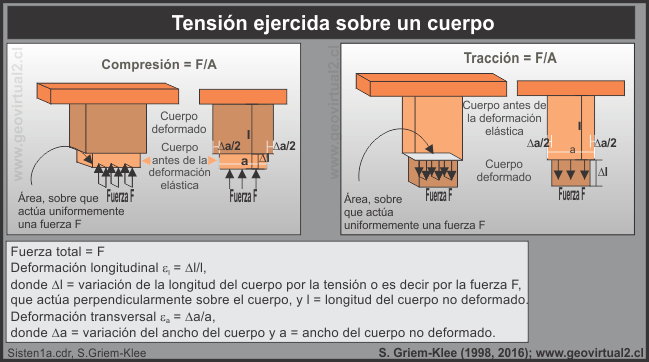
Tensión S se define como la fuerza F por unidad de área A: F/A, donde F
es la fuerza aplicada uniformemente a una pequeña superficie de área.
Presión o tracción se refiere a la tensión dirigida perpendicularmente al
área, según sea ejercida hacia el cuerpo sobre que actúa (presión) o en
sentido contrario (tracción). La presión causa un acortamiento en el interior
del cuerpo, en que actúa, la tracción produce un alargamiento en el interior
del cuerpo, en que actúa.
La deformación longitudinal εl
es la relación entre el alargamiento o el acortamiento Δ l
causado por una tensión y la longitud original l antes de la aplicación
de la tensión: ε l
= Δ l/l. La deformación transversal ε
a
se define como la relación entre la variación del ancho Δ
a causada por una tensión y el ancho primitivo a del cuerpo antes de la
aplicación de la tensión: ε
a =
Δ a/a.
Coeficiente de Poisson
Cuando un cuerpo se acorta por efecto de una compresión, se alarga en la
dirección perpendicular a la compresión. Un cuerpo alargado por efecto de
una tracción, disminuye su ancho en la dirección perpendicular a la tensión.
La relación entre la deformación longitudinal εl y la deformación
transversal εa se denomina coeficiente de Poisson σ .
σ =ε a/ ε l = (Δ a/a)/(Δ l/l).
Cuando una tensión actúa en un cuerpo en una dirección y el volumen del
cuerpo es constante, el coeficiente de Poisson tiene su valor máximo igual
a 0,5.
| Tipo de roca | Rango del coeficiente de Poisson s | |
| Roca consolidada, no alterada1 | 0,2 - 0,3 | |
| Roca sedimentaria clástica2 | 0,02 - 0,05 | |
| www.geovirtual2.cl | ||
1: Por ejemplo calizas de grano fino, rocas cristalinas.
2: Variando con la porosidad y el estado de meteorización.
Módulo de Young E
En el caso de tensiones de compresión o de tracción, que dan origen a una
deformación pequeña, la magnitud de esta deformación es proporcional a la
tensión según:
ε = k x S = (1/E) x S → S = E x ε ,
![]() ,
en donde
,
en donde
S = tensión
ε = deformación
E = constante de proporcionalidad y denominada módulo de YOUNG.
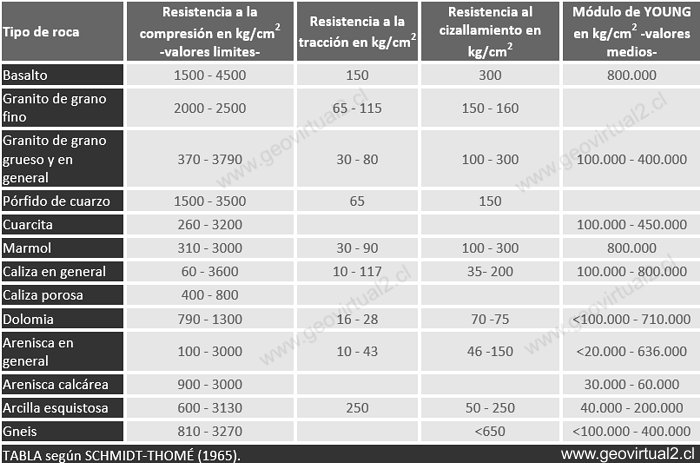
Para un sólido con un módulo de YOUNG E de valor numéricamente alto la deformación
causada por una tensión dada será menor en comparación a un sólido de E
de valor más pequeño. (Valores de E véase tabla).
Modulo de rigidez o de cizallamiento
El esfuerzo de cizallamiento se denomina la tensión, que actúa paralelamente
al área. El esfuerzo de cizallamiento da origen a una deformación por fractura.
La deformación por cizallamiento se expresa por el ángulo de deformación
F . El ángulo de deformación se forma por la superficie original del área
y la superficie deformada por la tensión ejercida paralelamente al área.
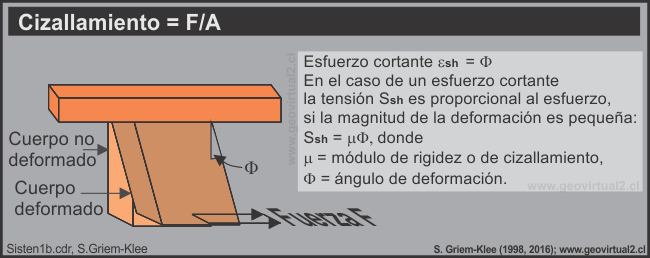
En el caso de un esfuerzo cortante y una deformación pequeña la tensión
Ssh es proporcional a la deformación: Ssh = m ´ f
. En esta relación m es la constante de proporcionalidad denominada módulo
de rigidez o de cizallamiento ɸ es el ángulo de deformación. Para los líquidos
vale µ = 0, para la mayoría de los demás materiales µ aproximadamente y
numéricamente vale la mitad de E.
Compresibilidad
y módulo volumétrico (véase fig.)
Considerando un cuerpo de volumen
V, que está sometido a una fuerza de compresión uniforme en todas las direcciones
y en consecuencia disminuirá su volumen en una cantidad
Δ V, la compresión ejercida sobre este
cuerpo es proporcional a la deformación o es decir a la relación entre la
variación del volumen y el volumen primitivo de este cuerpo antes de la
aplicación de la compresión según: Scompresión = k(Δ V/V),en
donde la constante de proporcionalidad k se denomina compresibilidad. El
valor recíproco de la compresibilidad 1/k = k' = Scompresión/(Δ
V/V) se denomina módulo volumétrico.
Existen las relaciones siguientes entre las constantes elásticas arriba
introducidas:
µ = /[ 2(1 + σ )] y k = E/[ 3(1 - 2σ)] ,
![]() véase
la figura siguiente.
véase
la figura siguiente.
Las ondas sísmicas se propagan en las sustancias sólidas de tal modo, que
la deformación de las partículas, que constituyen la sustancia sólida, pasan
por la sustancia con una velocidad, que depende de sus propiedades elásticas
y de su densidad.
Deformación (strain) por dilatación
Deformación por dilatación es la relación de la variación en la distancia
entre dos puntos distintos y separados (A y B), que se produce por un movimiento
de dilatación, y de la distancia original entre estos dos puntos.
Ondas sísmicas
Se distinguen las ondas sísmicas
internas y las ondas sísmicas superficiales.
Las ondas internas son:
● Ondas p u ondas longitudinales u ondas de compresión
● Ondas s u ondas transversales u ondas de cizalla
Las ondas superficiales son por ejemplo:
● Ondas de Love
● Ondas de Rayleigh
Ondas p u ondas longitudinales u ondas
de compresión
Las partículas de una onda p, longitudinal o de compresión oscilan en la
dirección de propagación de la onda. Las ondas p son parecidas a las ondas
sonoras ordinarias. Las ondas p son más rápidas que las ondas s o es decir
después un temblor en un observatorio primeramente llegan las ondas p, secundariamente
las ondas s. La velocidad de las ondas p se calcula como sigue:

Ondas s u ondas transversales u ondas
de cizalla
Las partículas de una onda s, transversal o de cizalla oscilan perpendicularmente
a la dirección de propagación. Se distingue las ondas sh, cuyas partículas
oscilan en el plano horizontal y perpendicular a la dirección de propagación,
y las ondas sv, cuyas partículas oscilan en el plano vertical y perpendicular
a la dirección de propagación. En las ondas s polarizadas sus partículas
oscilan en un único plano perpendicular a su dirección de propagación. La
velocidad de la onda s se calcula como sigue:

Ondas de Rayleigh
Rayleigh (1885) predijo la presencia de ondas superficiales diseñando matemáticamente
el movimiento de ondas planas en un espacio seminfinito elástico.
Las ondas de Rayleigh causan un movimiento rodante parecido a las ondas
del mar y sus partículas se mueven en forma elipsoidal en el plano vertical,
que pasa por la dirección de propagación. En la superficie el movimiento
de las partículas es retrógrado con respecto al avance de las ondas. La
velocidad de las ondas Rayleigh vRayleigh es menor que la velocidad de las
ondas s (transversales) y es aproximadamente vRaleigh = 0,9 ´ vs, según
DOBRIN (1988).
Ondas de Love
Love (1911) descubrió la onda superficial, que lleva su nombre estudiando
el efecto de vibraciones elásticas a una capa superficial.
Las ondas de Love requieren la existencia de una capa superficial de menor
velocidad en comparación a las formaciones subyacentes o es decir un gradiente
de velocidad positivo (velocidad se incrementa) con la profundidad. Las
ondas de Love son ondas de cizalla, que oscilan solo en el plano horizontal,
es decir las ondas de Love son ondas de cizalla horizontalmente polarizadas.
La velocidad de las ondas de Love es aproximadamente vLove =
0,9 x vs., según Doyle, (1995).
Las ondas internas se extienden en tres dimensiones. Las ondas superficiales
se extienden en solo dos dimensiones. Las velocidades de las ondas internas
y superficiales están relacionadas como sigue: vp > vs >
vLove > vRayleigh. Generalmente para las amplitudes
(A) de las ondas vale el orden inverso: ARayleigh > ALove >
As > Ap. Como las amplitudes de las ondas superficiales
se disminuyen con la profundidad del foco, la razón entre las amplitudes
de las ondas superficiales y las amplitudes de las ondas internas indica
aproximadamente la profundidad del foco.
En comparación con las ondas internas las amplitudes de las ondas superficiales
se disminuyen menos rápidamente con la distancia, en consecuencia en distancias
largas con respecto a un temblor las ondas superficiales generan señales
más altas y dominan los registros conservados en los sismógramas.
Las ondas superficiales están caracterizadas por la dispersión, o es decir
la velocidad de las ondas superficiales depende de su frecuencia y de su
longitud de onda. La variación de la velocidad con la frecuencia o la longitud
de onda se denomina dispersión. En una onda afectada por dispersión distintas
longitudes de onda se propagan con diferentes velocidades apareciendo como
un tren de eventos, cuyos ciclos sucesivos son de períodos incrementándose
o disminuyéndose.
Analizando la dispersión de las ondas de Rayleigh los científicos obtuvieron
informaciones muy útiles acerca de la estructura de la corteza terrestre
y del manto superior de la Tierra. En lo contrario en la exploración por
el método de reflexiones sísmicas las ondas de Rayleigh son menos útiles,
porque contribuyen apreciadamente al ruido del fondo.
Los parámetros característicos de las rocas, que se determina
con los métodos sísmicos son la velocidad de las ondas p y s, el coeficiente
de reflexión, la densidad. Propiedades de las rocas, que influyen estos
parámetros son entre otros:
● Petrografía, contenido en minerales.
● Estado de compacidad.
● Porosidad = porcentaje o proporción de espacio vacío (poros) en una roca.
● Relleno del espació vacío o es decir de los poros como aire, agua, petroleo,
gas.
● Textura y estructura de la roca.
● Temperatura.
● Presión.
Una variación en una de estas propiedades de la roca puede ser relacionada
por ejemplo con un límite entre dos estratos litológicos, con una falla
o una zona de fallas, con un cambio en el relleno del espacio poroso de
la roca.
Velocidades de las
ondas p y s de algunas rocas se presentan en la tabla siguiente:
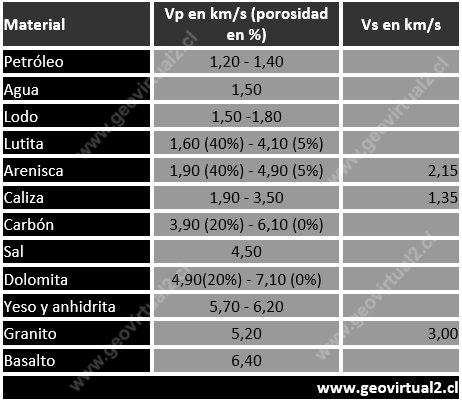
SHERIFF & GELDART, 1991 u otros.
Las ondas sísmicas internas como las ondas p y s son ondas elásticas, para
que valgan las leyes de la reflexión y de la refracción. Una onda sísmica
incidente en una superficie de separación entre dos medios como dos estratos
en parte es reflejada, en parte es refractada.
Las ondas sísmicas internas como las ondas p y s son ondas elásticas, para
que valgan las leyes de la reflexión y de la refracción. Una onda sísmica
incidente en una superficie de separación entre dos medios, como dos estratos,
en parte es reflejada, en parte es refractada. Para la reflexión vale la
ley de reflexión:

Cuando el ángulo de incidencia alcanza un valor crítico (Φ inc, para que
senΦ refracción = 90°), se genera una onda, que se propaga a lo largo de
la superficie de separación con la velocidad de la onda correspondiente
al estrato2. Esta onda se denomina onda de MINTROP, según Ludger Mintrop,
un alemán, quien en 1914 inventó el primero sismógrafo mecánico con precisión
suficiente para la exploración.
En los fenómenos de reflexión y de refracción se basan los dos distintos
métodos sísmicos: la sísmica de refracción y las reflexiones sísmicas
El comportamiento y la trayectoria de las ondas
sísmicas, que se propagan en el subsuelo se pueden presentar:
● Por un perfil, que incluye tiro y varios detectores (geófonos) alineados
en la superficie terrestre y que ilustra la penetración de los frentes de
onda o de los rayos de ondas respectivamente en las formaciones geológicas
del subsuelo.
● Por un gráfico del tiempo de la primera llegada de la onda sísmica en
función de la distancia desde el tiro hacia los geófonos, véase gráfico
distancia-tiempo.
Generando ondas sísmicas artificialmente (vibraciones mecánicas o vibraciones)
en o cerca de la superficie y observando su tiempo de llegada en las estaciones
de observación (geófonos) alineadas a lo largo de un perfil, se puede reconstruir
el recorrido de las ondas en el subsuelo y localizar discontinuidades como
límites litológicos o fallas.

Apuntes
- Geología
Contenidos
1. Introducción
2. Remote Sensing
3. Geoquímica
4. Métodos sísmicos
4.1 Sismología
4.2 Historia
4.3 Fundamentos
teóricos
4.4 ondas sísmicas
4.5 Método refracción
4.6 Método reflexión
4.7 Geófonos
4.8 Características
5. Método magnético
6. Método gravimétrico
7. Métodos eléctricos
Índice
Bibliografía
Páginas de Geología
Apuntes Geología General
Apuntes Geología Estructural
Apuntes
Depósitos Minerales
Colección de Minerales
Periodos y épocas
Figuras históricas
Citas geológicas
Exploración - Prospección
Módulo de Citas
Depósitos
Depósitos en el Mundo
Depósitos en Chile
Depósitos en Atacama
Bibliografía Depósitos Minerales
