Capitulo
6.2.
![]()
Contenido página
6.4 Gravimetría: Reducciones de datos - altura y Bouguer
4.4 Corrección para
la altura
La intensidad de la gravedad varía en relación inversa al cuadrado de la
distancia 'centro de la Tierra - estación de observación'. Refiriendo la
variación de la gravedad al modelo esférico de la Tierra en reposo el nivel
de referencia dista 6367,5km igual (al radio de la Tierra) con respecto
al centro de la Tierra.
Dgalt = 2 × f ×Mtierra/(rtierra)3
× a = a × 0,3083mgal/m, donde
● f = constante de gravitación = 6,67 × 10-8cm3g-1s-2,
● Mtierra = 5,977 × 1027g
● rtierra = 6367,5km
● a = altura sndm
Dgalt recibe un signo positivo para estaciones de observación
situadas encima del nivel de referencia. Dgalt lleva un signo
negativo para estaciones de observación ubicadas debajo del nivel de referencia.
Aplicando el modelo del elipsoide terrestre resultaría un valor de corrección,
que coincide con el valor introducido las tres primeras decimales. Para
lograr una precisión de 0,01mgal para las observaciones gravimétricas las
diferencias de altura con respecto al nivel de mar debería ser conocidas
con un error menor a 4cm.
Al efecto de la altura se denomina efecto de aire libre, puesto que las
masas de rocas presentes o no presentes entre el nivel de referencia y el
nivel de la estación de observación no lo influyen.
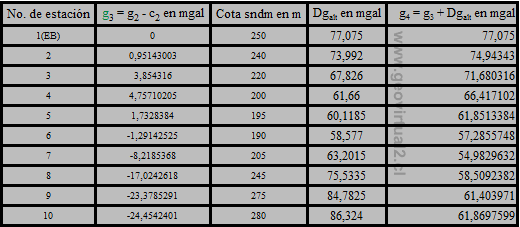
En el ejemplo se refiere la variación de la gravedad con la altura al nivel
de mar. Todas las estaciones de observación se ubican arriba del nivel de
mar. Por consiguiente se suma dgalt al valor de gravedad corregida para
la deriva, las mareas y la latitud g3 y se calcula: g4
= g3 + Dalt. Para la estación de observación No.6
por ejemplo la variación por la altura con respecto al nivel de mar es Dgalt
= 190m × 0,3083mgal/m = 58,577mgal. La anomalía de aire libre correspondiente
a la estación de observación No.6 es g4 = -1,29142525mgal + 58,577mgal
= 57,2855748mgal.
4.5 Corrección topográfica
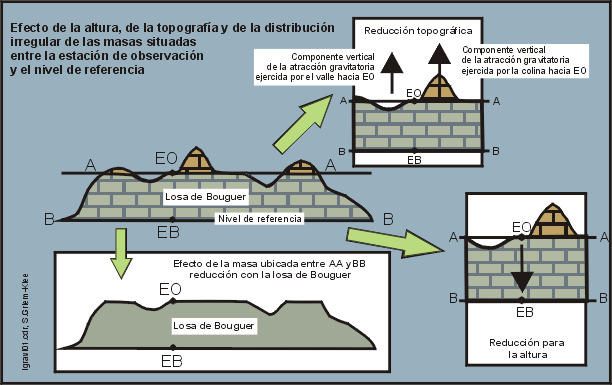
Un accidente de terreno elevado tal como una colina
ejercerá una atracción directamente proporcional a su densidad. Su componente
vertical estará dirigida hacia arriba y por consiguiente reducirá la gravedad
correspondiente a una estación de observación cercana. Por esto se debe
añadir el valor de su componente vertical al término de la gravedad observada
en la estación de observación. Una depresión como un valle es una masa negativa,
con su componente atractiva vertical dirigida hacia arriba. En este caso
también se añadirá el valor de la componente atractiva vertical del valle
al valor de gravedad observado en la estación de observación.
Se concluye que la corrección topográfica siempre lleva un signo positivo.
Además se debe aplicar la corrección topográfica al valor de referencia
medido en la estación de base. Según esto el valor de corrección topográfica
a sumar al valor de gravedad observado en una estación de observación se
calcula de modo siguiente: CTestación de observación - CTestación
de base.
La atracción de un accidente de terreno, sea de cota menor o mayor se disminuye
rápidamente con la distancia. Generalmente solo las estaciones de observación
muy cercanas o situadas directamente en una irregularidad topográfica requieren
una corrección topográfica.
4.6 Corrección con la losa de
Bouguer
La corrección con la losa de Bouguer elimina el efecto de las masas de rocas
ubicadas entre el nivel de referencia y la estación de observación. Las
masas de rocas ejercen una atracción gravitatoria extra a una estación de
observación situada en una altura mayor a aquella de la estación de base.
El incremento esperado de la atracción gravitatoria debido a las rocas ubicándose
entre el nivel de referencia y el nivel de la estación de observación a
menudo se modela utilizando el hipótesis que se puede aproximar la roca
con una losa horizontal de dimensiones infinitas y de densidad uniforme,
cuyo piso coincide con el nivel de referencia y cuyo techo está en el nivel
de la estación de observación. Se emplea la formula siguiente para cuantificar
el efecto de Bouguer:
DgBouguer = 2 × (3,14159) × f × d × a = 0,04191 ×d × a [en mgal], donde
f = constante de gravitación = 6,67 × 10-8cm3g-1s-2,
d = densidad de las masas de rocas ubicándose entre el nivel de referencia
y el nivel de la estación de observación en g/cm3,
a = diferencia de altura entre el nivel de referencia y el nivel de la estación
de observación en m.
La corrección con la losa de Bouguer DgBouguer se resta del valor
observado en una estación de observación en el caso que la estación de observación
está encima de la estación de base. Se la suma al valor observado en el
caso que la estación de observación se sitúa debajo del nivel de referencia.
Referente a los signos, la corrección para la altura o es decir de aire
libre siempre lleva el signo opuesto al signo aplicado para la corrección
con la losa de Bouguer.
La corrección con la losa de Bouguer se basa en una densidad uniforme, que
se supone para las masas rocosas ubicadas entre el nivel de referencia y
el nivel de la estación de observación. La mayoría de los casos reales no
cumple esta condición. Por ejemplo en un área sedimentaria construida por
una secuencia de estratos horizontales de distintas densidades se puede
modificar la formula para la corrección de Bouguer de la manera siguiente:
DgBouguer = 0,04191 (d1 × a1 + d2
× a2 + d3 × a3 +... +... + di
× ai) mgal, donde
d1 a di = densidades de los estratos 1 a i,
a1 a ai = anchos (potencias) de los estratos
1 a i.
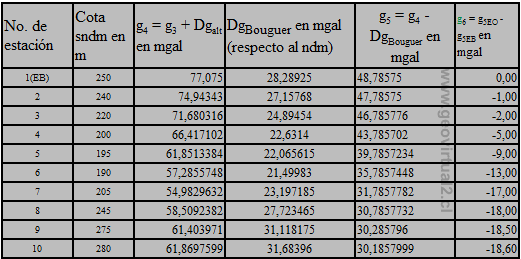
La densidad media del área sea 2,7g/cm3. En el primer paso se realiza la
corrección con la losa de Bouguer con respecto al nivel de mar. Por consiguiente
la potencia de la losa de Bouguer coincide con las cotas correspondientes
a las estaciones de observación. Como cada una de las estaciones se ubica
sobre el nivel de mar se debe restar la corrección con la losa de Bouguer
del valor de gravedad corregida para la deriva, las mareas, la latitud y
la altura g4 y la anomalía de Bouguer con respecto al nivel de mar es g5
= g4 - DgBouguer. Para la estación de observación 7 se obtiene por ejemplo:
DgBouguer = 0,04191 × 2,7g/cm3 × 205m = 23,197185mgal.
g5 = 54,9829632mgal - 23,197185mgal = 31,7857782mgal
La variación de la anomalía de Bouguer con respecto a la estación de base
g6 se calcula como sigue: g6 = g5EO - g5EB,
donde EO = estación de observación y EB = estación de base.
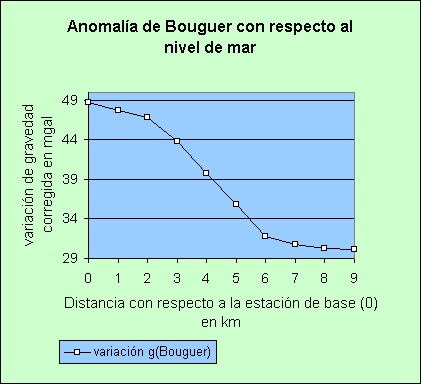
El grafico ilustra la anomalía de Bouguer en función de la distancia con
respecto al nivel de mar. Comparándolo con el
perfil morfológico correspondiente no
se nota ninguna correlación. Para una curva de tal forma existen varias
interpretaciones (en preparación). Cuál de estas interpretaciones semeja
más a la realidad se deberá comprobar por medio de otros estudios geofísicos
y/o geológicos.
La figura siguiente ilustra el efecto de las reducciones
para la altura, topográfica y con la losa de Bouguer.
4.7 Anomalías de gravedad
Una anomalía de gravedad se define como la variación de los valores medidos
de la gravedad con respecto a la gravedad normal después de haber aplicado
las correcciones necesarias.
La anomalía de aire libre resulta de las correcciones de la influencia de
las mareas, de la derive del instrumento de medición, de la latitud y de
la altura.
La anomalía de Bouguer se obtiene aplicando todas las correcciones mencionadas.

Apuntes
- Geología
Contenidos Exploración Minera
1. Introducción
2. Remote Sensing
3. Geoquímica en prospección
4. Métodos sísmicos
5. Método magnético
6. Método gravimétrico
Introducción gravimetría
Reducción
datos (1)
Reducción de datos
(2)
●
Reducción de datos (3)
Densidad
Métodos y
instrumentos
Interpretaciones
7. Métodos eléctricos
Índice
Bibliografía
Páginas de Geología
Apuntes Geología General
Apuntes Geología Estructural
Apuntes
Depósitos Minerales
Colección de Minerales
Periodos y épocas
Figuras históricas
Citas geológicas
Exploración - Prospección
Módulo de Citas
Depósitos
Depósitos en el Mundo
Depósitos en Chile
Depósitos en Atacama
Bibliografía Depósitos Minerales
