Geología Estructural: Proyección estereográfica

Contenido página: Uso de la proyección con pliegues

1. Introducción:

Capaz una de las más importantes aplicaciones relacionadas a la proyección estereográfica es la interpretación y visualización de rocas plegadas y deformadas plásticamente. Como áreas plegadas muestran una simetría altamente compleja, junto con escalas que podrían escapar de una visualización simple en terreno, muchas veces la proyección estereográfica es la única herramienta para mostrar o visualizar estas estructuras tan complejas.
¿Cuáles son las problemas generales en rocas plegadas?

a) Buzamientos (manteos) diferentes en las rocas.
b) Diferentes direcciones de inclinación.
c) Rumbo circular si el eje del pliegue muestra una inclinación.
d) El conjunto de pliegues y una morfología viva.
e) Dimensiones de las estructuras muy variables entre milímetros hasta decenas de kilómetros.
f) Superposición de varios tipos de pliegues en el mismo sector.

En resumen se puede decir que en áreas de mediana y alta complejidad los valores tomados con la brújula no muestran una pauta interpretable, es decir variaciones de rumbo, del manteo, de la dirección de inclinación tan inesperadas que una interpretación o visualización sin herramientas como la proyección estereográfica casi es imposible.

2. Apariencia de pliegues en la Red de Schmidt:

Los elementos más importantes de un pliegue en su uso en la proyección estereográfica son:
1. Eje del pliegue
2. Actitudes (valores dirección/manteo) de las unidades geológicas deformadas
3. Foliaciones como esquistosidades etc.

Diferencia entre áreas plegadas y comportamiento frágil (fallas):



Al primero es importante relacionar a los datos obtenidos a un ambiente general de deformación: Dúctil y frágil (o los dos). Ambientes frágiles (A en la figura) producen generalmente "nubes" de polos - cada nube corresponde a una estructura planar (puede ser falla, diaclasa, veta, dique etc.) con una cierta variación de la estructura por irregularidades naturales.
Ambientes dúctiles - entonces rocas plegadas se caracterizan por la presencia de sets de datos en forma circulo máximo. Aunque muchas veces se nota el circulo máximo bien rudimentario.


Pliegues se define bastante bien por su eje. El eje del pliegue es un elemento linear, una lineación - en pliegues de escala pequeña (milímetros, centímetros) se puede medir directamente en terreno (con ayuda de un lápiz) - pero en situaciones de escala mediana o grande la proyección estereográfica es una gran ayuda. Hay que recordarse que estructuras de medianos o grandes dimensiones escapan en terreno muchas veces de un análisis directo por falta de una visión general.
El eje del pliegue generalmente se ubica en un ángulo de 90° en distancia de todas las proyecciones de las líneas normales de los estratos que forman el pliegue.
Entonces si se detectó un (rudimentario) circulo máximo en sus datos tectónicos compuesto de las mismas foliaciones (generalmente estratos) es muy probable, que eso corresponde a un pliegue. El polo correspondiente a este círculo máximo sería el eje del pliegue [el polo se encuentra en 90° de distancia de todos los estratos]. Es la misma relación polo a su círculo máximo en elementos planares como fallas.


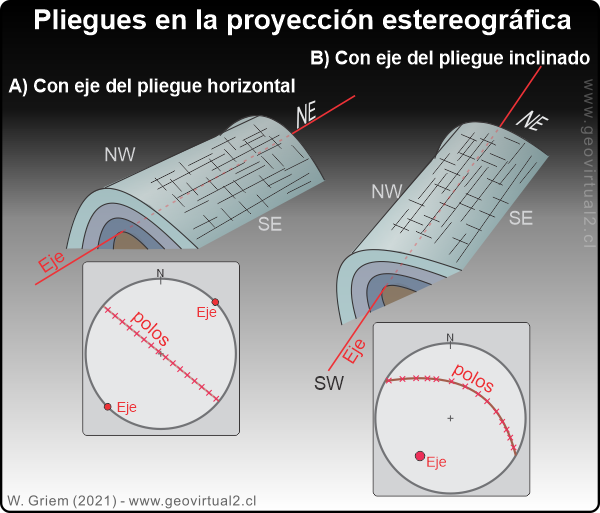
Un detalle para recordar: en "A", donde el eje del pliegue es horizontal, se nota que el eje se encuentra dos veces en la proyección. Hay que imaginarse la proyección como esfera, es decir los polos o elementos que se encuentran encima del margen exterior igualmente se encuentra al lado opuesto - es el mismo valor. Como el eje es una lineación y lineaciones horizontales se ubican encima del margen - un eje horizontal aparece dos veces.

3. Como se interpreta un pliegue en la proyección estereográfica?

Como pliegues de dimensiones grandes (pueden llegar a varios kilómetros) escapan a nuestra visión general es sumamente importante realizar un análisis del pliegue en base a los datos obtenidos en terreno. En la figura 3 se graficó a los datos de un pliegue con eje inclinado. Llama atención que todos los valores de los estratos plegados en su conjunto forman un círculo máximo. El polo del eje del pliegue se ubica en 225/25LIN es decir el eje se inclina hacia Suroeste con 25° de plunge (es como el manteo para lineaciones).
Los flancos del pliegue (con manteos más verticales) se ubican más al margen de la proyección. ¡Pero cuidado! - Como esos flancos, como el círculo máximo es una construcción de muchos estratos (hay que recordarse que ese circulo máximo es un producto de muchas mediciones de estratos, de estratificación - entonces de elementos planares -"planos" donde se usa la línea normal y finalmente se ubican al lado opuesto). Entonces en ese ejemplo el Flanco Noroeste se encuentra en la proyección abajo en el cuadrante que uno relaciona con Sureste - pero correctamente son los valores del flanco noroeste. Lo mismo ocurre con el flanco sureste - se quedó en la proyección en la parte superior.

La charnela del pliegue (donde el pliegue muestra su menor manteo) en ese caso de un pliegue con eje inclinado (figura arriba) no es horizontal (en pliegues con ejes horizontales sería horizontal, es decir el circulo máximo intercepta el chinche en el medio). En pliegues con eje inclinado se puede confirmar que el sector de la menor inclinación de los estratos plegados corresponde con el plunge del eje del pliegue. Ese valor se puede tomar en dos formas: Desde el circulo máximo hacia el chinche en su punto más cercano. La otra forma sería desde el polo del eje del pliegue hasta el contorno de la proyección.