Capítulo
11 / 2
Contenidos de la
página
Introducción
Preparación de la hoja
Ingreso de planos
Ingreso de lineaciones
Lectura de lineaciones
Computacional
- - -
Página
anterior -
próxima
---
Contenidos Estructural
Más geovirtual
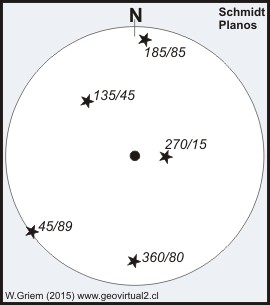
Ejemplos de algunos valores de planos en la proyección Schmidt - hemisferio abajo (siempre salen "vice-versa")
Inglés:
Rumbo: strike
Manteo o buzamiento: dip
Dirección de inclinación: Dip direction
Alemán
Rumbo: Die Streichrichtung
Manteo: Das Einfallen
Dirección de Inclinación: Die Einfallsrichtung
Definición:
Rumbo: Es la línea resultante
de una intersección de un plano horizontal con un plano inclinado.
Lineaciones
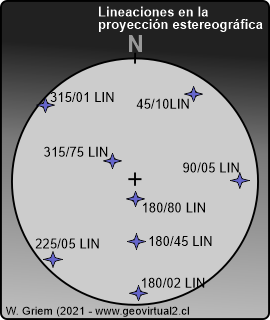
Ejemplos de lineaciones en la proyección estereográfica - los polos se ubican "como se piensa" - "como esperado".
Contenido página: Preparación de la hoja ● Ingreso de planos ● Ingreso de lineaciones ● computacional
1. Uso de la proyección
estereográfica, red de Schmidt:
El uso de la proyección estereográfica en papel "artesanal" todavía tiene
algunas ventajas, especialmente para aprender cómo funciona, pero con pocos
datos (10 o menos) es más rápido en comparación del uso de un programa computacional.
Además, algunos programas computacionales no trabajan como deseado - existen
trampas y fácilmente se comete errores. Por eso antes de usar un programa
siempre hay que hacer una comparación de algunos datos procesados en el
computador con los mismos datos procesados en una forma "artesanal" en papel.
Sí coinciden ambas versiones no hay problemas.
La
proyección estereográfica es una herramienta en la geología y minería
muy poderosa. Permite graficar, presentar, analizar e
interpretar un sin número de situaciones donde principalmente elementos
tectónicos (planares y lineaciones como estratos, vetas, fallas, estrías
entre otros) forman una relación. La proyección permite alumbrar
relaciones 3-dimensionales y determinar los valores específicos,
concretos. El campo de acción es casi infinito, existen un sin-número de
situaciones donde la proyección estereográfica ofrece un apoyo.
Cierto, no siempre es fácil trabajar con la proyección, especialmente en
el comienzo nos cuesta imaginarnos las situaciones y sumergir al mundo
3-dimensional. Nos cuesta entender todas las etapas y definiciones en
algunas tareas. Por eso se recomienda trabaja paso a paso. Es decir se
"desarma" a los problemas y se trata generar un listado de pasos
consecutivos para resolver el problema.
Algunos pasos casi
siempre se repiten en el uso de la proyección:
a) Preparación de la hoja (es obvio...) [aquí más]
b) Ingreso de planos como polos [fallas, estratos etc. saldrán en la proyección como un
puntito no más] [aquí más]
c) Ingreso de
lineaciones a la proyección [ojo: Siempre tenemos claro que es una
lineación y que es un plano !!!!] [aquí más]
d) Interpretación de una lineación [lo viceversa del anterior - tengo un
polo que representa una lineación - como se obtiene el valor]
[aquí más]
e) Construcción del circulo máximo [el circulo
máximo es una línea generalmente curvada que se ubica en 90° de
distancia] [aquí más]
En continuación se presenta a los procedimientos de esas etapas,
después se discute algunos problemas que se puede resolver con la proyección
estereográfica.
1.1 Preparación de la hoja
Para ingresar puntos a la red de Schmidt se necesita la pauta (Original
de la red), un papel transparente (diamante, mantequilla, poliéster etc.)
un chinche (¡no el animal! - de metal con cabeza plana).
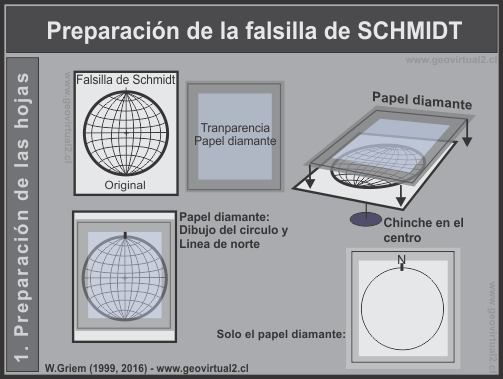 Figura 1: Preparación de las hojas
de la proyección de Schmidt: Figura 1: Preparación de las hojas
de la proyección de Schmidt:a) Pauta original Schmidt b) Chinche c) Papel transparente |
2. Ingreso de los planos
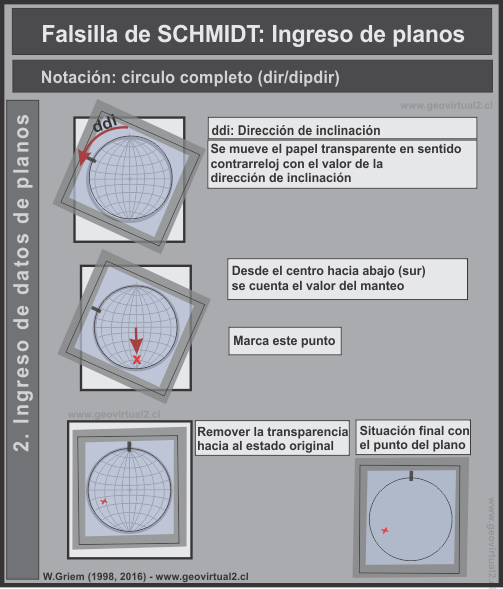 Figura 2: Figura 2:Ingreso de planos en el sistema Dip/Dipdirection: a) se gira del valor dip en sentido contrarrelaoj b) se cuenta el manteo entre chinche hacia abajo (sur). c) Se marca el punto d) Se mueve la transparencia al estado original. |
3. Ingreso de lineaciones
Para recordarse lineaciones son líneas
en la naturaleza, igualmente son elementos tectónicos que requieren un
tratamiento en la proyección estereográfica [véase lineaciones,
definición y ejemplos]. En el ambiente geológico existen lineaciones
"reales" visibles, naturales como estrías o minerales orientados. pero
también existen lineaciones como resultado de otros elementos
tectónicos, por ejemplo las intersecciones de dos planos. Igualmente
existen lineaciones "artificiales" como perforaciones o túneles.
Uno
de los objetivos principales de la proyección estereográfica es la
visualización de una relación entre elementos planares como fallas
tectónicas por ejemplo y elementos lineales (lineaciones) como estrías
por ejemplo. Al primero aquí la parte "técnica" como se ingresa a una
lineación a la proyección de Schmidt.
Al primero recuérdese que una
lineación requiere dos cifras para su definición de su orientación en un
ambiente Tres-dimensional: El Trend y el Plunge; [donde el Trend es algo
como la dirección azimutal de la línea y el plunge algo como manteo de
la línea]. Pero vamos a usar siempre las palabras Trend y Plunge. Una
lineación que se inclina hacia Sureste con 45° entonces tiene un valor
de 135/45 LIN.
El ingreso de estos valores es muy fácil y en
cierta manera parecida a un plano. Pero OJO !!!!!! - Nunca, nunca jamás
vamos a equivocarnos Plano es un plano - Lineaciones es una Lineación.
Entonces, el ingreso de una lineación se realiza en siguiente forma:
A) Se gira la transparencia al sentido contrarreloj por
el valor del Trend (la dirección azimutal del elemento lineal)
B) En esa posición, y ojo aquí viene la diferencia a
respeto de los planos, se cuenta el Plunge (el "manteo") de la lineación
desde el Norte hacia el centro (al chinche).
Como resultado sale
un polo (un punto) que representa la orientación 3-Dimensional de la
lineación. Donde se puede destacar:
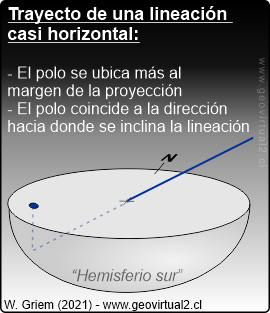
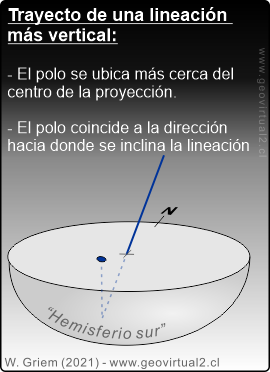
1. Lineaciones verticales
o casi verticales (como pozos o perforaciones verticales) deben ubicarse
en el centro, en el medio de la proyección estereográfica. Lineaciones
más horizontales se ubican en la cercanía del margen de la proyección.
2. Las lineaciones se ubican en la proyección "como esperado"
o "como uno piensa". Una lineación que se inclina hacia al norte debe
ubicarse en la proyección como Punto en el sector Norte de la
Proyección.
Por ejemplo un túnel, una rampa que se inclina hacia
Noreste con un ángulo de 10° debería proyectarse como polo o punto en la
parte NE de la proyección y bien cerca del margen.
En la figura abajo se grafica el procedimiento de
ingreso de lineaciones a la proyección estereográfica:
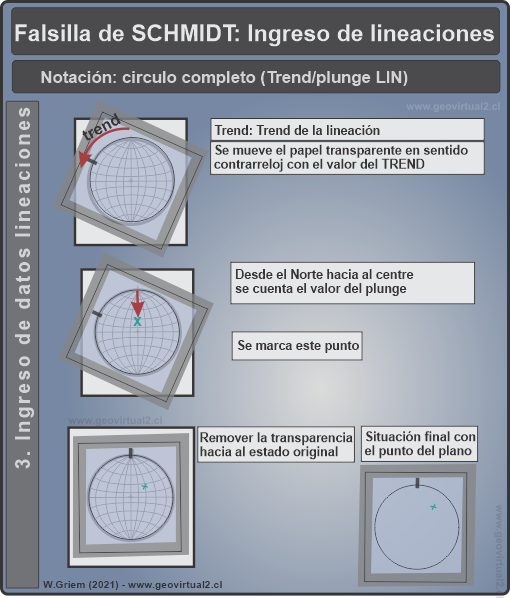 Figura
2: Figura
2:Ingreso de Lineaciones o elementos lineares - A) Se gira al sentido contrarreloj por el valor del Trend. B) se cuenta el valor Plunge desde NORTE hacia al centro. |
Resumen y anotaciones:
a) Siempre trabaja consciente - que es lineación diferenciar bien de un
elemento planar.
b) Elementos planares / "planos" se ubican en la
proyección "viceversa" o "al lado contrario" como uno piensa.
c)
Elementos lineares o lineaciones siempre se ubican como "uno piensa" -
Línea que apunta al norte se queda con un puntito hacia al norte en la
proyección.
Muchas veces, capaz más frecuente, es la
identificación de lineaciones. En muchas situaciones el resultado es una
lineación (por ejemplo la intersección de dos elementos planares como
dos vetas - el resultado es la traza de la intersección que corresponde
a una lineación. Por eso muchas veces es importante interpretar una
lineación identificada en la proyección. Es decir - tengo el punto y
como se puede determinar a base de ese punto los valores del Trend y
Plunge de la lineación correspondiente.
4 Lectura de lineaciones

El caso más común es que el proyecto conduce a lineaciones como
resultado. En ese caso se debe tomar la lectura de la lineación. La
lineación en la proyección estereográfica aparece como un punto o polo.
Igualmente, este polo contiene toda la información tres dimensional. Es
decir, a partir de la ubicación de este polo en la Red de Schmidt de
puede llegar a los valores determinados de ese lineación [Trend/Plunge].
Se recomienda:
A) Estimación del polo "Lineaciones
se ubican como esperado" - en el ejemplo arriba entonces como 135/20 LIN
B) Se gira la transparencia hasta la lineación se ubica encima del eje
de lectura, es decir eje Norte-Chinche.
C) Se cuenta contrarreloj la
distancia entre Norte (transparente) y Norte (fotocopia).
D) En la
misma posición se cuenta desde el Norte hacia al Chinche el plunge.
E) Se compara calor estimado con el valor tomado.
Se recomienda
este procedimiento porque el nivel de equivocación es ese paso es
sumamente alto.
Computación:
Hoy día se usa generalmente programas computacionales para realzar trabajos
con la proyección estereográfica. La ventaja es impresionante por eso las
proyecciones de la red de Wulff o red de Schmidt eran unos de los pioneros
en el uso de la informática - durante una época donde realmente era difícil
encontrar una aplicación útil para computadores.
El ingreso de los datos no siempre es fácil. Al primero hay que verificar
que tipo de datos espere el programa. Significa puede ser "tipo americano",
"medio circulo" o circulo completo. Más encima hay que verificar la forma
de los datos (puede ser por ejemplo 198/34 o 34 - 198). Además, hay que
verificar el programa espera datos de 400 o de 360º. Se recomienda de realizar
una "marcha blanca" con algunos tres o cuatro datos para verificar como
se quedan y eliminar problemas antes del ingreso de un set de 2000 datos.
Algunos programas antiguos o versiones antiguas (por ejemplo, DIPs 3) necesitan
un "editor" es decir un pequeño programa para ingresar los datos con el
formato "txt". Hay que cumplir 100% el formato pedido por el programa, especialmente
el cabezal y el fin. En este caso se recomienda el uso de un set de datos
antiguos - guardando bajo otro nombre - borrando los datos antiguos y reemplazando
con los datos nuevos.
El ingreso de los datos tectónicos toma su tiempo. Un buen estudio puede
llegar a 4000 y más datos. La manera más eficiente y seguro es el uso de
notaciones con pocos dígitos, por ejemplo la notación del
circulo completo. Un plano corresponde a 2 (dos!) números. La
notación tipo americana pide el ingreso de 5 números o letras.

Contenido Tectónica
1. Capítulo: Planos y Brújula
2.
Capítulo: Foliaciones
3. Capitulo: Lineaciones
4. Capitulo: Fallas tectónicas
5. Capitulo: Pliegues
6. Capitulo: Otros elementos
7. Capitulo: Cronología
8. Cap.: Modelos Geotectónicos (*)
9. Capítulo: Fuerza y deformaciones
Practicas:
10. Levantamiento tectónico
11. Proyección estereográfica
Idea de la proyección
►
Manejo de la proyección
Circulo máximo
Intersección de planos
Medir ángulos de distancia
Lineación y plano - una relación
Perforación y estratos
Proyección y pliegues
12. Roseta de
diaclasas
13. Bibliografía y enlaces
Pauta Schmidt
![]()
You Tube canal
Videos en estructural
Introducción a la proyección estereográfica
Idea de la proyección estereografica
![]()
Historia de las geociencias y minería
Rumbo manteo y dirección
Derrumbe de una mina (Simonin, 1869)
Páginas de Geología
![]()
Apuntes Geología General
Apuntes Geología Estructural
Apuntes
Depósitos Minerales
Colección de Minerales
Periodos y épocas
Figuras históricas
Citas geológicas
Índice
de palabras
Bibliografía
Fotos: Museo Virtual

