Geología Estructural: Diagramas y estadísticas

Contenido página: Intersección de dos planos  "artesanal" ● computación

Red de Schmidt (Falsilla de Schmidt)
Intersección de dos planos

Dos planos (no paralelos) se interceptan. La intersección es una lineación - una línea. Un ejemplo sería las paredes de una sala. La intersección de dos paredes será el rincón. Este rincón se puede describir como una línea vertical y es el resultado de las dos paredes. En la geología en algunos casos la intersección de dos planos marca una línea de alta importancia. Por ejemplo la situación típica en los yacimientos históricos en la Región Atacama (Chile) - la intersección de dos vetas en el sector Chañarcillo o Tres Puntas eran los sectores más ricos en plata - se llamaba "cruceros". Hasta hoy día este fenómeno es visible en muchos yacimientos actuales. Véase Apuntes Depósitos Minerales.

Identificación de la intersección:
Los dos planos ya están en la proyección (ejemplo f1 y f2) como polo (x) y como circulo máximo (figura 3). Lógicamente, donde se cruzan los círculos máximos se "ubica" la intersección. No hay que olvidar que la palabra "ubicación" se refiere a una orientación en un espacio tres dimensional.



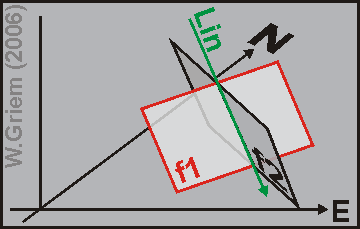Figura 1:
Dos planos se interceptan y forman una lineación. Lineaciones tienen igual que planos una dirección de inclinación y un manteo solamente se llama trend (corresponde a la dirección) y plunge (corresponde al manteo).

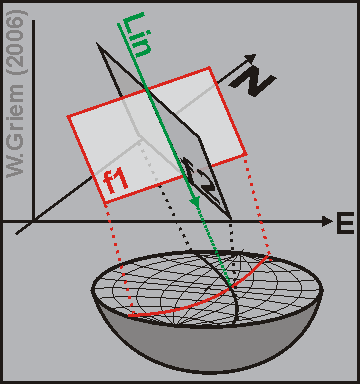Figura 2: Los dos planos y la lineación se puede proyectar a la red de Schmidt.

Como la Red de Schmidt originalmente tenía el objetivo de calcular lineaciones todo el procedimiento de llegar a un número es muy fácil:

1. Lineaciones se ubican "como se piensa". Una lineación inclinándose hacía al sur sería un punto en el sector sur de la proyección. Una lineación vertical sería un punto en el centro. Entonces en el ejemplo (dibujo 1) f1 y f2 se interceptan en el sector ENE con un manteo bien vertical (muy cerca del centro). 
Para llegar a los valores precisos hay que hacer siguiente maniobra:

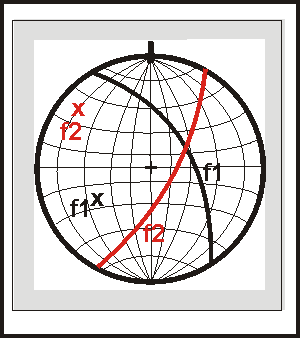Figura 3: Situación inicial. f1 y f2 se interceptan en el sector ENE en poca distancia del centro - significa un manteo alto. Se puede estimar entonces un valor de 80/70

1. Moviendo la transparencia hasta que la intersección se queda encima del eje "Norte - Centro"
2. La "dirección de inclinación" (correcto es la palabra "trend" - por que es una lineación) se toma en la distancia entre Norte(copia proyección) hacía N(transparencia) en el sentido contrarreloj!
3. El "manteo" (correcto es la palabra "plunge" - porque es una lineación)  corresponde a la distancia entre Norte e intersección (Ejemplo: la flecha azul "mt")

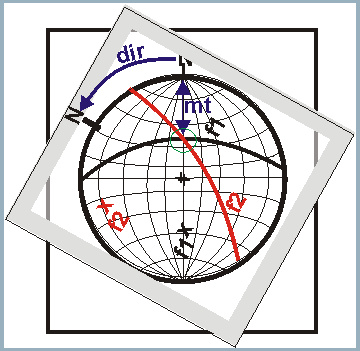Figura 4:
Se giró la transparencia hasta que se quedó la intersección justamente encima el eje Norte - centro. La dirección de la inclinación de la lineación corresponde a la distancia N(pauta arriba) hasta N transparencia - tomada siempre contrarreloj.


Programas computacionales:
La toma de lineaciones en los programas computacionales es mucho más fácil:
Simplemente se hace "clic" encima de la intersección - o el programa automáticamente muestra el valor sí el mouse está encima del punto. Pero cuidado: hay que verificar los datos. Probablemente el programa muestra los datos de un supuesto plano y no de una lineación. Por eso siempre hay que primero estimar el valor, para prevenir lecturas erróneas. Como ya mencionado lineaciones tienen una ubicación en la proyección "como se piensa" entonces es fácil realizar una estimación rápida (véase).