Capítulo
11 / 3
Contenidos de la
página
Circulo máximo
- - -
Página
anterior -
próxima
---
Contenidos Estructural
Más geovirtual
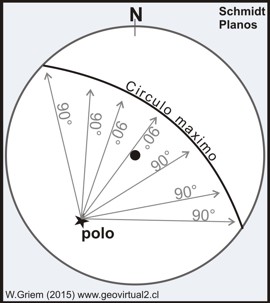
La línea máxima se ubica en todo su trayecto en distancia de 90° al polo
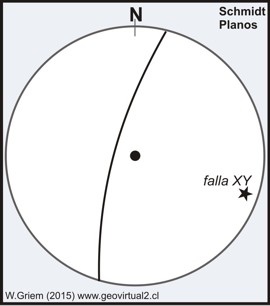
Ejemplo 1: Una falla ("XY") de orientación 280/80 - con su circulo máximo respectivo.
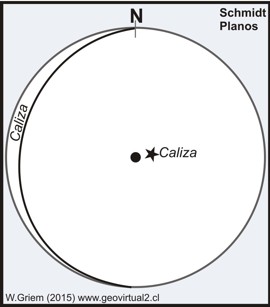
Ejemplo 2: La caliza muestra la orientación 270/10, e circulo máximo se ubica en 90° de distancia
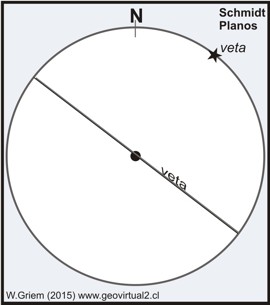
Ejemplo 3: Una veta(casi vertical) con los datos 225/89 - el circulo máximo se encuentra casi como línea recta traspasando el centro.
Inglés:
Rumbo: strike
Manteo o buzamiento: dip
Dirección de inclinación: Dip direction
Alemán
Rumbo: Die Streichrichtung
Manteo: Das Einfallen
Dirección de Inclinación: Die Einfallsrichtung
Definición:
Rumbo: Es la línea resultante
de una intersección de un plano horizontal con un plano inclinado.
Contenido página: Circulo máximo
Proyección (Red) de Schmidt (Falsilla de Schmidt)
Construcción del "Circulo máximo"
1. Idea:
La relación entre un polo y su circulo máximo siempre, por definición,
son 90°. Es decir el circulo máximo marca a todos los puntos que están
en 90° de distancia al polo. Mejor se entiende eso en en caso de planos
como fallas o estratos (véase un poco más abajo).
El circulo máximo es la proyección del plano entero a la red de Schmidt.
Significa como resultado sale una línea desde un borde hacia el otro, con
una distancia de 180º
El circulo máximo solamente es una otra manera de proyectar un plano geológico.
La ventaja del circulo máximo al respeto del
polo (punto) de una línea normal es: El circulo máximo es más fácil
para interpretar y la base de algunos interpretaciones avanzadas. La desventaja
del circulo máximo es que la transparencia solamente permite el dibujo de
algunos 5 hacia 10 círculos. Con una cantidad mayor no se ve nada.
Por eso normalmente se ingresan los datos como
polo (punto) de la línea normal (véase:
línea normal), después se juntan los elementos en "nubes de puntos"
con un promedio - un máximo - gráfico (Se aplica la red de conteo y isolineas
para definir el punto medio de la distribución, el punto o polo principal)
y para estos puntos principales (promedios) se buscan el circulo máximo
correspondiente. Es decir, se busca el "promedio gráfico" de una acumulación
de puntos, y solamente este valor - el promedio se traduce a un circulo
máximo.
Figura 1: Visualización de los
dos ejemplos más frecuentes del uso del circulo máximo.
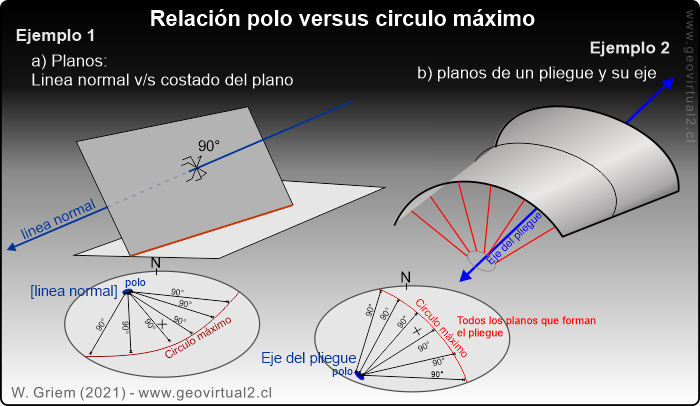
Figura: Los ejemplos más comunes (ojo, hay más) son el
circulo máximo como representante de un elemento planar (estrato, falla,
veta entre otros) - donde se entiende la distancia entre el polo de la
línea normal y el costado del plano son 90°. Más concreto 90° en muchas
direcciones (se puede medir infinitas cantidades de 90° entre plano y
línea normal - es decir el polo que representa el plano en su forma como
línea normal es una manera en definir un plano en un espacio
3-Dimanesional; la otra forma es el circulo máximo.
El otro ejemplo
grafica la relación de un pliegue con su eje. Todos los estratos que
forman un pliegue se ubican en una distancia de 90°. Entonces como el
eje es una lineación, se grafica como un polo de lineación - los
estratos - con sus líneas normales de este pliegue teóricamente deberían
formar un circulo máximo. Como las líneas normales de los estratos
formadores del pliegue se ubican en un ángulo de 90° de distancia.
Entonces este círculo máximo del pliegue es un conjunto con muchas
líneas normales (en realidad, matemáticamente serían infinitas) que en
su totalidad forman el círculo máximo. Más adelante se analizará para
que sirve esta metodología.
2. Búsqueda del circulo máximo:
Un plano geológico y la línea normal de este plano tienen una diferencia
de 90º a todos lados los lados. Significa que el punto o polo que sale en
la proyección (como resultado de la línea normal) tiene una distancia de
90º al círculo máximo del mismo plano. La tarea es la búsqueda de una línea
en la proyección estereográfica cual tiene siempre una distancia de 90º
hacia al punto / polo.
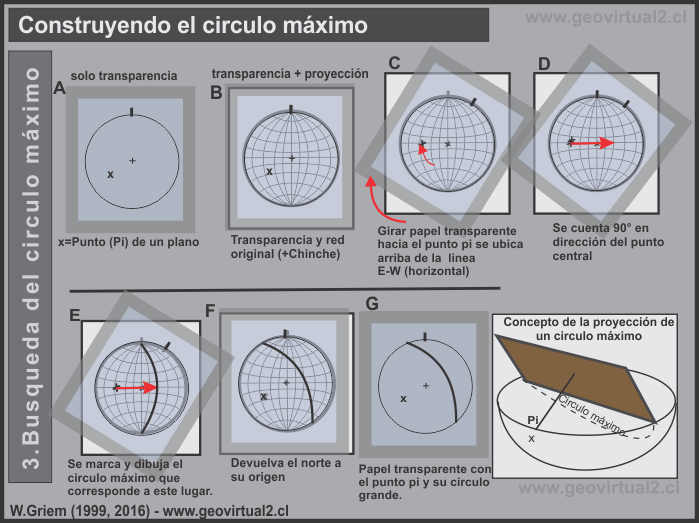
Figura 1:
A - C) se gira la transparencia hasta que el polo se ubica encima del eje
E -W, puede ser centro - E o centro - W.
D) se cuenta 90º de distancia a lo largo del eje E -W, traspasando el chinche.
E) Resulta un punto, que sirve como punto de inicio del circulo máximo -
el circulo máximo entero se pauta de la hoja original de la proyección estereográfica.
F) se gira la transparencia a su orientación original (Norte arriba)
G) se saca la pauta original de la proyección.
La ventaja del circulo máximo es su fácil interpretación:
- un circulo máximo recto corresponde a un plano vertical, la orientación
en la proyección corresponde a la orientación en la naturaleza.
- un circulo máximo curvado corresponde a un plano con una cierta inclinación.
La curva siempre marca hacia la dirección de inclinación (en el ejemplo
arriba entonces NE).
-la distancia entre el centro (chinche) y curva corresponde al manteo. Significa
planos verticales o subverticales tienen una ubicación muy cercana del centro.
Planos casi-horizontales tienen una curva muy amplia, ubicándose cerca del
margen.
- Planos horizontales coinciden con el margen.
Además el circulo máximo es la base de
muchos aplicaciones avanzadas - por ejemplo:
a) La intersección de dos círculos máximos corresponde con
la línea de intersección en la realidad.
b) Tres planos - entonces tres círculos máximos pueden formar una cuña.
c) Socavones, piques, túneles corresponden a lineaciones - se puede graficar
la simetría entre los labores y elementos tectónicos - para planificar el
trayecto más conveniente de los futuros labores.
d) perforaciones y anclajes corresponden también a lineaciones - se puede
buscar la manera más segura y más eficiente de instalar un sistema de anclajes.
e) reconocimiento de mega-estructuras tectónicas como pliegues: Un circulo
máximo no solamente proyecta un plano, el circulo máximo también puede coincidir
con un set de datos tomados en un pliegue. Para entender pliegues de gran
escala - especialmente con eje inclinado ayuda bastante la proyección estereográfica.
Pauta Schmidt

Contenido Tectónica
1. Capítulo: Planos y Brújula
2.
Capítulo: Foliaciones
3. Capitulo: Lineaciones
4. Capitulo: Fallas tectónicas
5. Capitulo: Pliegues
6. Capitulo: Otros elementos
7. Capitulo: Cronología
8. Cap.: Modelos Geotectónicos (*)
9. Capítulo: Fuerza y deformaciones
Practicas:
10. Levantamiento tectónico
11. Proyección estereográfica
Idea de la proyección
Manejo de la proyección
Lineaciones en la proyección
►
Circulo máximo
Intersección de planos
Medir ángulos de distancia
Lineación y plano - una relación
Perforación y estratos
Proyección y pliegues
12. Roseta de
diaclasas
13. Bibliografía y enlaces
Pauta Schmidt
![]()
Historia de las geociencias y minería
Rumbo manteo y dirección
Derrumbe de una mina (Simonin, 1869)
Páginas de Geología
![]()
Apuntes Geología General
Apuntes Geología Estructural
Apuntes
Depósitos Minerales
Colección de Minerales
Periodos y épocas
Figuras históricas
Citas geológicas
Índice
de palabras
Bibliografía
Fotos: Museo Virtual

